Capitolul III
Reprezentarea informaţiilor cu obiecte

3.1 Obiecte
3.2 Încapsularea informaţiilor în interiorul obiectelor
3.3 Clase de obiecte
3.4 Derivarea claselor de obiecte
3.5 Interfeţe spre obiecte

3.1 Obiecte

Informaţiile pe care le reprezentăm în memoria calculatorului sunt rareori atât de simple precum culorile sau literele. În general, dorim să reprezentăm informaţii complexe, care să descrie obiectele fizice care ne înconjoară sau noţiunile cu care operăm zilnic, în interiorul cărora culoarea sau o secvenţă de litere reprezintă doar o mică parte. Aceste obiecte fizice sau noţiuni din lumea reală trebuiesc reprezentate în memoria calculatorului în aşa fel încât informaţiile specifice lor să fie păstrate la un loc şi să se poată prelucra ca un tot unitar. Să nu uităm însă că, la nivelul cel mai de jos, informaţia ataşată acestor obiecte continuă să fie tratată de către compilator ca un şir de numere naturale, singurele informaţii reprezentabile direct în memoria calculatoarelor actuale.

Pentru a reprezenta în memoria internă obiecte fizice sau noţiuni, este nevoie să izolăm întregul set de proprietăţi specifice acestora şi să îl reprezentăm prin numere. Aceste numere vor ocupa în memorie o zonă compactă pe care, printr-un abuz de limbaj, o vom numi, într-o primă aproximare, obiect. Va trebui însă să aveţi întotdeauna o imagine clară a deosebirii fundamentale dintre un obiect fizic sau o noţiune şi reprezentarea acestora în memoria calculatorului.

De exemplu, în memoria calculatorului este foarte simplu să creăm un nou obiect, identic cu altul deja existent, prin simpla duplicare a zonei de memorie folosite de obiectul pe care dorim să-l dedublăm. În realitate însă, este mult mai greu să obţinem o copie identică a unui obiect fizic, fie el o simplă foaie de hârtie sau o bancnotă de 10000 de lei.

Să revenim însă la numerele naturale. Din moment ce ele sunt singurele entităţi reprezentabile în memoria calculatorului, este firesc ca acesta să fie echipat cu un set bogat de operaţii predefinite de prelucrare a numerelor. Din păcate, atunci când facem corespondenţa dintre numere şi litere de exemplu, nu ne putem aştepta la un set la fel de bogat de operaţii predefinite care să lucreze cu litere. Dar, ţinând cont de faptul că în cele din urmă lucrăm tot cu numere, putem construi propriile noastre operaţii specifice literelor, combinând în mod corespunzător operaţiile numerice predefinite.

De exemplu, pentru a obţine dintr-o literă majusculă, să spunem ‘A’, corespondenta ei minuscul㠑a’, este suficient să adunăm un deplasament numeric corespunzător, presupunând că literele mari şi cele mici sunt numerotate în ordine alfabetică şi imediat una după cealaltă în convenţia de reprezentare folosită. În setul ASCII deplasamentul este 32, reprezentarea lui ‘A’ fiind 65 iar reprezentarea lui ‘a’ fiind 97. Acest deplasament se păstrează pentru toate literele din alfabetul englez şi român, la cel din urmă existând totuşi o excepţie în cazul literei ‘Ş’.

Putem să extindem cerinţele noastre mai departe, spunând că, atunci când analizăm un obiect fizic sau o noţiune pentru a le reprezenta în calculator, trebuie să analizăm nu numai proprietăţile acestora dar şi modul în care acestea pot fi utilizate şi care sunt operaţiile care pot fi executate asupra lor sau cu ajutorul lor. Acest set de operaţii va trebui ulterior să-l redefinim în contextul mulţimii de numere care formează proprietăţile obiectului din memoria calculatorului, şi să îl descompunem în operaţii numerice preexistente. În plus, trebuie să analizăm modul în care reacţionează obiectul atunci când este supus efectului unor acţiuni exterioare. Uneori, setul de operaţii specifice unui obiect împreună cu modul în care acesta reacţionează la stimuli exteriori se numeşte comportamentul obiectului.

De exemplu, dacă dorim să construim un obiect care reprezintă o minge de formă sferică în spaţiu, este necesar să definim trei numere care să reprezinte coordonatele x, y şi z relativ la un sistem de axe dat, precum şi o valoare pentru raza sferei. Aceste valori numerice vor face parte din setul de proprietăţi ale obiectului minge. Dacă mai târziu vom dori să construim o operaţie care să reprezinte mutarea în spaţiu a obiectului minge, este suficient să ne folosim de operaţiile cu numere pentru a modifica valorile coordonatelor x, y şi z.

Desigur, obiectul minge este insuficient descris prin aceste coordonate şi, pentru a simula în calculator obiectul real este nevoie de multe proprietăţi suplimentare precum şi de multe operaţii în plus. Dar, dacă problema pe care o avem de rezolvat nu necesită aceste proprietăţi şi operaţii, este preferabil să nu le definim în obiectul folosit pentru reprezentare. Rezultatul direct al acestui mod de abordare este acela că vom putea defini acelaşi obiect real în mai multe feluri pentru a-l reprezenta în memoria internă. Modul de definire depinde de problema de rezolvat şi de programatorul care a gândit reprezentarea. De altfel, aceste diferenţe de percepţie ale unui obiect real există şi între diverşi observatori umani.

Din punctul de vedere al programării, un obiect este o reprezentare în memoria calculatorului a proprietăţilor şi comportamentului unei noţiuni sau ale unui obiect real.

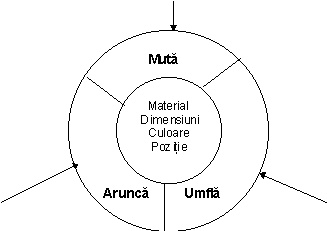
Figura 3.1 Modelul de reprezentare al unui obiect în memorie. Stratul exterior reprezintă doar operaţiile care oferă calea de a interacţiona cu proprietăţile obiectului şi nu are corespondent direct în zona de memorie ocupată de obiect.

3.2 Încapsularea informaţiilor în interiorul obiectelor

Există situaţii în care accesul din exterior la proprietăţile unui obiect poate să pună probleme acestuia. Ce s-ar întâmpla de exemplu dacă s-ar putea accesa direct valorile care definesc funcţionalitatea corpului uman? Desigur, există cazuri în care acest lucru ar fi îmbucurător. N-ar mai fi nevoie să acţionăm indirect asupra concentraţiilor de enzime în corp ci am putea să modificăm aceste valori în mod direct. Dar, în acelaşi timp, am putea provoca mari necazuri în cazul în care am modifica aceste valori în afara pragului suportabil de către organism. Din aceste motive, este preferabil să lăsăm modificarea acestor parametri în sarcina exclusivă a unor operaţii definite de către obiect, operaţii care vor verifica noile valori înainte de a le schimba în interiorul obiectului. În lipsa acestui filtru, putem să stricăm coerenţa valorilor memorate în interiorul unui obiect, făcându-l inutilizabil.

Din acest punct de vedere, putem privi obiectul ca pe un set de valori care formează miezul obiectului şi un set de operaţii care îmbracă aceste valori, protejându-le. Vom spune că proprietăţile obiectului sunt încapsulate în interiorul acestora. Mai mult, obiectul încapsulează şi modul de funcţionare a operaţiilor lui specifice, din exterior neputându-se observa decât modul de apelare a acestor operaţii şi rezultatele apelurilor. Cu alte cuvinte, procesul de încapsulare este procesul de ascundere a detaliilor neimportante sau sensibile de construcţie a obiectului.

Dar nu numai proprietăţile unui obiect trebuiesc protejate ci şi operaţiile definite de către acesta. Unele dintre operaţiile definite pentru un obiect, cum ar fi de exemplu procesul respirator al omului, sunt periculos de lăsat la dispoziţia oricui. Este preferabil să putem controla foarte exact cine ce operaţii poate apela pentru un anumit obiect. În acest mod, din punctul de vedere al unui observator străin, omul este perceput ca un obiect mult mai simplu decât este în realitate, pentru că acel observator nu poate vedea decât acele valori şi nu poate apela decât acele operaţii care sunt făcute publice.

Desigur, în practică este nevoie de o oarecare rafinare a gradului de protejare a fiecărei operaţii sau proprietăţi în aşa fel încât însuşi accesul observatorilor exteriori să poată fi nuanţat în funcţie de gradul de similitudine şi apropiere al observatorului faţă de obiectul accesat. Rafinarea trebuie să meargă până la a putea specifica pentru fiecare proprietate şi operaţie în parte care sunt observatorii care au acces şi care nu.

Această protejare şi încapsulare a proprietăţilor şi operaţiilor ce se pot executa cu ajutorul unui obiect are şi o altă consecinţă şi anume aceea că utilizatorul obiectului respectiv este independent de detaliile constructive ale obiectului respectiv. Structura internă a obiectului poate fi astfel schimbată şi perfecţionată în timp fără ca funcţionalitatea de bază să fie afectată.

3.3 Clase de obiecte

În lumea reală se pot identifica uşor familii de obiecte. Este greu să descriem într-un limbaj de programare fiecare minge din lume dar, pentru a putea folosi orice minge din lume, este suficient să descriem o singură dată care sunt proprietăţile unei mingi în general, precum şi operaţiile care pot fi executate cu aceasta. Aceasta nu înseamnă că toate obiectele minge din lume sunt identice. Diferenţa dintre ele se află reprezentată în primul rând în valorile proprietăţilor lor care sunt mărimi numerice variabile, adică diferă de la un obiect de acelaşi fel la altul. De exemplu, în fiecare obiect minge vom avea un număr natural care reprezintă culoarea mingii. Acest număr poate să difere de la o minge la alta exact aşa cum, în realitate, culoarea diferă de la o minge la alta. La fel coordonatele poziţiei mingii la un moment dat sau raza mingii precum şi materialul din care este confecţionată au valori care variază de la o minge la alta.

Cu alte cuvinte, fiecare minge din lume are acelaşi set de proprietăţi, dar valorile acestora pot să difere de la o minge la alta. Modelul de reprezentare în memorie a unui obiect este întotdeauna acelaşi, dar valorile memorate în locaţiile corespunzătoare proprietăţilor sunt în general diferite.

În ceea ce priveşte operaţiile, acestea sunt întotdeauna aceleaşi dar rezultatul aplicării lor poate să difere în funcţie de valorile proprietăţilor obiectului asupra căruia au fost aplicate. De exemplu, atunci când aruncăm o minge spre pământ ea va ricoşa din acesta ridicându-se din nou în aer. Înălţimea la care se va ridica însă, este dependentă de dimensiunile şi materialul din care a fost confecţionată mingea. Cu alte cuvinte, noua poziţie în spaţiu se va calcula printr-o operaţie care va ţine cont de valorile memorate în interiorul obiectului. Se poate întâmpla chiar ca operaţia să hotărască faptul că mingea va străpunge podeaua în loc să fie respinsă de către aceasta.

Să mai observăm că operaţiile nu depind numai de proprietăţile obiectului ci şi de unele valori exterioare acestuia. Atunci când aruncăm o minge spre pământ, înălţimea la care va ricoşa aceasta depinde şi de viteza cu care a fost aruncată mingea. Această viteză este un parametru al operaţiei de aruncare. Nu are nici un rost să transmitem ca parametrii ai unei operaţii valorile proprietăţilor unui obiect pentru că acestea sunt întotdeauna disponibile operaţiei. Nici o operaţie nu se poate aplica asupra unui obiect fără să ştim exact care este obiectul respectiv şi ce proprietăţi are acesta. Este absurd să ne gândim la ce înălţime se va ridica o minge în general, fără să facem presupuneri asupra valorilor proprietăţilor acesteia. Să mai observăm însă că, dacă toate mingile ar avea aceleaşi valori pentru proprietăţile implicate în operaţia descrisă mai sus, am putea să calculăm înălţimea de ricoşeu în general, fără să fim dependenţi de o anumită minge.

În concluzie, putem spune că obiectele cu care lucrăm fac parte întotdeauna dintr-o familie mai mare de obiecte cu proprietăţi şi comportament similar. Aceste familii de obiecte le vom numi în continuare clase de obiecte sau concepte în timp ce obiectele aparţinând unei anumite clase le vom numi instanţe ale clasei de obiecte respective. Putem vorbi despre clasa de obiecte minge şi despre instanţele acesteia, mulţimea tuturor obiectelor minge care există în lume. Fiecare instanţă a clasei minge are un loc bine precizat în spaţiu şi în timp, un material şi o culoare. Aceste proprietăţi diferă de la o instanţă la alta, dar fiecare instanţă a aceleiaşi clase va avea întotdeauna aceleaşi proprietăţi şi aceleaşi operaţii vor putea fi aplicate asupra ei. În continuare vom numi variabile aceste proprietăţi ale unei clase de obiecte şi vom numi metode operaţiile definite pentru o anumită clasă de obiecte.

Pentru a clarifica, să mai reluăm încă o dată: O clasă de obiecte este o descriere a proprietăţilor şi operaţiilor specifice unui nou tip de obiecte reprezentabile în memorie. O instanţă a unei clase de obiecte este un obiect de memorie care respectă descrierea clasei. O variabilă a unei clase de obiecte este o proprietate a clasei respective care poate lua valori diferite în instanţe diferite ale clasei. O metodă a unei clase este descrierea unei operaţii specifice clasei respective.

Să mai precizăm faptul că, spre deosebire de variabilele unei clase, metodele acesteia sunt memorate o singură dată pentru toate obiectele. Comportarea diferită a acestora este dată de faptul că ele depind de valorile variabilelor.

O categorie aparte a claselor de obiecte este categoria acelor clase care reprezintă concepte care nu se pot instanţia în mod direct, adică nu putem construi instanţe ale clasei respective, de obicei pentru că nu avem destule informaţii pentru a le putea construi. De exemplu, conceptul de om nu se poate instanţia în mod direct pentru că nu putem construi un om despre care nu ştim exact dacă este bărbat sau femeie. Putem în schimb instanţia conceptul de bărbat şi conceptul de femeie care sunt nişte subconcepte ale conceptului om.

Clasele abstracte, neinstanţiabile, servesc în general pentru definirea unor proprietăţi sau operaţii comune ale mai multor clase şi pentru a putea generaliza operaţiile referitoare la acestea. Putem, de exemplu să definim în cadrul clasei de obiecte om modul în care acesta se alimentează ca fiind independent de apartenenţa la conceptul de bărbat sau femeie. Această definiţie va fi valabilă la amândouă subconceptele definite mai sus. În schimb, nu putem decât cel mult să precizăm faptul că un om trebuie să aibă un comportament social. Descrierea exactă a acestui comportament trebuie făcută în cadrul conceptului de bărbat şi a celui de femeie. Oricum, este interesant faptul că, indiferent care ar fi clasa acestuia, putem să ne bazăm pe faptul că acesta va avea definit un comportament social, specific clasei lui.

Cele două metode despre care am vorbit mai sus, definite la nivelul unui superconcept, sunt profund diferite din punctul de vedere al subconceptelor acestuia. În timp ce metoda de alimentaţie este definită exact şi amândouă subconceptele pot să o folosească fără probleme, metoda de comportament social este doar o metodă abstractă, care trebuie să existe, dar despre care nu se ştie exact cum trebuie definită.

Fiecare dintre subconcepte trebuie să-şi definească propriul său comportament social pentru a putea deveni instanţiabil. Dacă o clasă de obiecte are cel puţin o metodă abstractă, ea devine în întregime o clasă abstractă şi nu poate fi instanţiată, adică nu putem crea instanţe ale unei clase de obiecte abstracte.

Altfel spus, o clasă abstractă de obiecte este o clasă pentru care nu s-au precizat suficient de clar toate metodele astfel încât să poată fi folosită în mod direct.

3.4 Derivarea claselor de obiecte

O altă proprietate interesantă a claselor de obiecte este aceea de ierarhizare. Practic, ori de câte ori definim o nouă clasă de obiecte care să reprezinte un anumit concept, specificăm clasa de obiecte care reprezintă conceptul original din care provine noul concept împreună cu diferenţele pe care le aduce noul concept derivat faţă de cel original. Această operaţie de definire a unei noi clase de obiecte pe baza uneia deja existente o vom numi derivare. Conceptul mai general se va numi superconcept iar conceptul derivat din acesta se va numi subconcept. În acelaşi mod, clasa originală se va numi superclasă a noii clase în timp ce noua clasă de obiecte se va numi subclasă a clasei derivate.

Uneori, în loc de derivare se foloseşte termenul de extindere. Termenul vine de la faptul că o subclasă îşi extinde superclasa cu noi variabile şi metode.

În spiritul acestei ierarhizări, putem presupune că toate clasele de obiecte sunt derivate dintr-o clasă iniţială, să-i spunem clasa de obiecte generice, în care putem defini proprietăţile şi operaţiile comune tuturor obiectelor precum ar fi testul de egalitate dintre două instanţe, duplicarea instanţelor sau aflarea clasei de care aparţine o anumită instanţă.

Ierarhizarea se poate extinde pe mai multe nivele, sub formă arborescentă, în fiecare punct nodal al structurii arborescente rezultate aflându-se clase de obiecte. Desigur, clasele de obiecte de pe orice nivel pot avea instanţe proprii, cu condiţia să nu fie clase abstracte, imposibil de instanţiat.

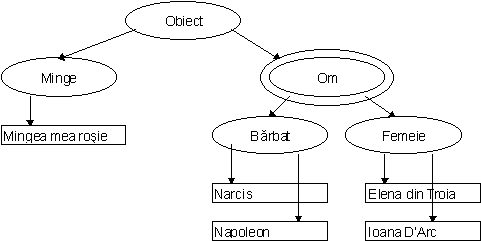
Figura 3.2 O ierarhie de clase de obiecte în care clasele sunt reprezentate în câmpuri eliptice iar instanţele acestora în câmpuri dreptunghiulare. Clasele abstracte de obiecte au elipsa dublată.

Desigur, este foarte dificil să construim o ierarhie de clase de obiecte completă, care să conţină clase de obiecte corespunzătoare fiecărui concept cunoscut. Din fericire, pentru o problemă dată, conceptele implicate în rezolvarea ei sunt relativ puţine şi pot fi uşor izolate, simplificate şi definite. Restrângerea la minimum a arborelui de concepte necesar rezolvării unei anumite probleme fără a se afecta generalitatea soluţiei este un talent pe care fiecare programator trebuie să şi-l descopere şi să şi-l cultive cu atenţie. De alegerea acestor concepte depinde eficienţa şi flexibilitatea aplicaţiei.

O clasă de obiecte derivată dintr-o altă clasă păstrează toate proprietăţile şi operaţiile acesteia din urmă aducând în plus proprietăţi şi operaţii noi. De exemplu, dacă la nivelul clasei de obiecte om am definit forma bipedă a acestuia şi capacitatea de a vorbi şi de a înţelege, toate acestea vor fi moştenite şi de către clasele derivate din clasa om, şi anume clasa bărbaţilor şi cea a femeilor. Fiecare dintre aceste clase de obiecte derivate îşi vor defini propriile lor proprietăţi şi operaţii pentru a descrie diferenţa dintre ele şi clasa originală.

Unele dintre proprietăţile şi operaţiile definite în superclasă pot fi redefinite în subclasele de obiecte derivate. Vechile proprietăţi şi operaţii sunt disponibile în continuare, doar că pentru a le putea accesa va trebui să fie specificată explicit superclasa care deţine copia redefinită. Operaţia de redefinire a unor operaţii sau variabile din interiorul unei clase în timpul procesului de derivare o vom numi rescriere.

Această redefinire ne dă de fapt o mare flexibilitate în construcţia ierarhiei unei probleme date pentru că nici o proprietate sau operaţie definită într-un punct al ierarhiei nu este impusă definitiv pentru conceptele derivate din acest punct direct sau nu.

Revenind pentru un moment la protejarea informaţiilor interne ale unui obiect să precizăm faptul că gradul de similitudine de care vorbeam mai sus este mărit în cazul în care vorbim de două clase derivate una din cealaltă. Cu alte cuvinte, o subclasă a unei clase are acces de obicei la mult mai multe informaţii memorate în superclasa sa decât o altă clasă de obiecte oarecare. Acest lucru este firesc ţinând cont de faptul că, uneori, o subclasă este nevoită să redefinească o parte din funcţionalitatea superclasei sale.

3.5 Interfeţe spre obiecte

Un obiect este o entitate complexă pe care o putem privi din diverse puncte de vedere. Omul de exemplu poate fi privit ca un mamifer care naşte pui vii sau poate fi privit ca o fiinţă gânditoare care învăţă să programeze calculatoare sau poate fi privit ca un simplu obiect spaţio-temporal care are propria lui formă şi poziţie în funcţie de timp.

Această observaţie ne spune că trebuie să dăm definiţii despre ce înseamnă cu adevărat faptul că un obiect poate fi privit ca un mamifer sau ca o fiinţa gânditoare sau ca un obiect spaţio-temporal. Aceste definiţii, pe care le vom numi în continuare interfeţe, sunt aplicabile nu numai clasei de obiecte om dar şi la alte clase de obiecte derivate sau nu din acesta, superclase sau nu ale acesteia. Putem să găsim o mulţime de clase de obiecte ale căror instanţe pot fi privite ca obiecte spaţio-temporale dar care să nu aibă mare lucru în comun cu omul. Practic, atunci când construim o interfaţă, definim un set minim de operaţii care trebuie să aparţină obiectelor care respectă această interfaţă. Orice clasă de obiecte care declară că respectă această interfaţă va trebui să definească toate operaţiile.

Operaţiile însă, sunt definite pe căi specifice fiecărei clase de obiecte în parte. De exemplu, orice obiect spaţial trebuie să definească o operaţie de modificare a poziţiei în care se află. Dar această operaţie este diferită la un om, care poate să-şi schimbe singur poziţia, faţă de o minge care trebuie ajutată din exterior pentru a putea fi mutată. Totuşi, dacă ştim cu siguranţă că un obiect este o instanţă a unui clase de obiecte care respectă interfaţa spatio-temporală, putem liniştiţi să executăm asupra acestuia o operaţie de schimbare a poziţiei, fără să trebuiască să cunoaştem amănunte despre modul în care va fi executată această operaţie. Tot ceea ce trebuie să ştim este faptul că operaţia este definită pentru obiectul respectiv.

În concluzie, o interfaţă este un set de operaţii care trebuiesc definite de o clasă de obiecte pentru a se înscrie într-o anumită categorie. Vom spune despre o clasă care defineşte toate operaţiile unei interfeţe că implementează interfaţa respectivă.

Cu alte cuvinte, putem privi interfeţele ca pe nişte reguli de comportament impuse claselor de obiecte. În clipa în care o clasă implementează o anumită interfaţă, obiectele din clasa respectivă pot fi privite în exclusivitate din acest punct de vedere. Interfeţele pot fi privite ca nişte filtre prin care putem privi un anumit obiect, filtre care nu lasă la vedere decât proprietăţile specifice interfeţei, chiar dacă obiectul în vizor este mult mai complicat în realitate.

Interfeţele crează o altă împărţire a obiectelor cu care lucrăm. În afară de împărţirea normală pe clase, putem să împărţim obiectele şi după interfeţele pe care le implementează. Şi, la fel cu situaţia în care definim o operaţie doar pentru obiectele unei anumite clase, putem defini şi operaţii care lucrează doar cu obiecte care implementează o anumită interfaţă, indiferent de clasa din care acestea fac parte.