Capitolul II
Limbaje de programare

2.1 Comunicaţia om-maşină
2.2 Tipuri de numere reprezentabile în calculator
2.3 Valori de adevăr
2.4 Şiruri de caractere
2.5 Tipuri primitive de valori ale unui limbaj de programare
2.6 Tablouri de elemente
2.7 Expresii de calcul
2.8 Variabile
2.9 Instrucţiuni

2.1 Comunicaţia om-maşină

Pentru a executa un program de calculator este necesar să putem comunica cu unitatea centrală pentru a-i furniza instrucţiunile necesare. Cel mai simplu mod de a le comunica este înscrierea codului instrucţiunilor direct în memoria calculatorului de unde pot fi citite de către unitatea centrală. Această cale este însă extrem de anevoioasă pentru programator pentru că el trebuie să înveţe să se exprime coerent într-un limbaj ale cărui componente de bază sunt coduri numerice.

O alternativă mai bună este folosirea unui limbaj de comunicaţie format dintr-un număr foarte mic de cuvinte şi caractere speciale împreună cu un set de convenţii care să ajute la descrierea numerelor şi a operaţiilor care trebuiesc executate cu aceste numere. Limbajul trebuie să fie atât de simplu încât calculatorul să poată traduce singur, prin intermediul unui program numit compilator, frazele acestui limbaj în instrucţiuni ale unităţii centrale. Ori de câte ori vom imagina un nou limbaj de comunicaţie cu calculatorul va trebui să creăm un nou program compilator care să traducă acest limbaj în instrucţiuni ale unităţii centrale, numite uneori şi instrucţiuni maşină.

În realitate folosirea termenului de limbaj de comunicaţie nu este extrem de fericită pentru că de obicei noi doar instruim calculatorul ce are de făcut şi cum trebuie să facă acel lucru, fără să-i dăm vreo şansă acestuia să comenteze sarcinile primite. În continuare vom numi aceste limbaje simplificate limbaje de programare pentru a le deosebi de limbajele pe care le folosim pentru a comunica cu alţi oameni şi pe care le vom numi limbaje naturale.

Limbajele de programare trebuie să ne ofere o cale de descriere a modulului în care dorim să reprezentăm informaţiile cu care lucrează programul, o cale de a specifica operaţiile care trebuiesc executate cu aceste informaţii şi o cale de a controla ordinea în care sunt executate aceste operaţii.

În plus, limbajele de programare trebuie să respecte următorul principiu fundamental: rezultatul execuţiei unei comenzi dintr-un limbaj de programare trebuie să fie complet determinat. Asta înseamnă că în limbajele de programare nu este permisă nici o formă de ambiguitate a exprimării.

Informaţiile reprezentate în memoria calculatorului şi prelucrate de către un program scris într-un limbaj de programare se numesc date. Tipurile de date care se pot descrie direct cu un anumit limbaj de programare se numesc tipurile de date elementare ale limbajului. Operaţiile elementare posibil de exprimat într-un limbaj de programare se numesc instrucţiuni ale limbajului.

Limbajele de programare au evoluat foarte mult de la începuturile calculatoarelor. Tendinţa generală este aceea de apropiere treptată de limbajele naturale şi de modul în care acestea descriu şi utilizează informaţiile. Abstracţiile exprimabile cu ajutorul limbajelor de programare sunt din ce în ce mai multe şi cuprind o gamă din ce în ce mai largă a noţiunilor fundamentale cu care operează mintea umană.

Un alt aspect în care se reflectă evoluţia limbajelor de programare este reprezentat de creşterea profunzimii şi calităţii controlului pe care compilatoarele îl fac în momentul traducerii din limbaj de programare în limbaj maşină, astfel încât şansa de a greşi la descrierea programului să fie cât mai mică.

Cu toate că limbajele de programare au făcut paşi esenţiali în ultimul timp, ele au rămas totuşi foarte departe de limbajele naturale. Pentru a programa un calculator, trebuie să poţi gândi şi să poţi descrie problemele într-unul dintre limbajele pe care acesta le înţelege. Din acest motiv, scrierea programelor continuă să rămână o activitate rezervată unui grup de iniţiaţi, chiar dacă acest grup este în continuă creştere.

2.2 Tipuri de numere reprezentabile în calculator

Deşi toate informaţiile reprezentabile direct în memoria calculatorului sunt doar numere naturale, constructorii calculatoarelor de astăzi au diversificat tipurile acestora prin stabilirea unor convenţii de reprezentare pentru numerele negative, reale şi pentru caractere. Aceste convenţii folosesc numerele naturale pentru reprezentarea celorlalte tipuri de numere. Uneori, reprezentările ocupă mai mult de un octet în memoria calculatorului, dimensiunile obişnuite fiind 1, 2, 4 sau 8 octeţi. Sau, echivalent, 8, 16, 32 sau 64 de biţi.

Numerele naturale sunt întotdeauna pozitive. Pentru reprezentarea unui număr întreg cu semn pot fi folosite două numere naturale. Primul dintre acestea, având doar două valori posibile, reprezintă semnul numărului şi se poate reprezenta folosind o singură cifră binară. Dacă valoarea acestei cifre binare este 0, numărul final este pozitiv, iar dacă valoarea cifrei este 1, numărul final este negativ. Al doilea număr natural folosit în reprezentarea numerelor întregi cu semn conţine valoarea absolută a numărului final. Această convenţie, deşi are dezavantajul că oferă două reprezentări pentru numărul zero, un zero pozitiv şi altul negativ, este foarte aproape de reprezentarea numerelor cu semn folosită de calculatoarele moderne.

În realitate, convenţia care se foloseşte pentru reprezentarea numerelor întregi cu semn este aşa numita reprezentare în complement faţă de doi. Aceasta reprezintă numerele negative prin complementarea valorii lor absolute bit cu bit şi apoi adunarea valorii 1 la numărul rezultat. Complementarea valorii unui bit se face înlocuind valoarea 1 cu 0 şi valoarea 0 cu 1. Dacă avem de exemplu numărul 1, reprezentat pe un octet ca un şir de opt cifre binare 00000001, complementarea bitcu bit a acestui număr este numărul reprezentat pe un octet prin11111110.

Pentru a reprezenta valoarea -1 nu ne mai rămâne altceva de făcut decât să adunăm la numărul rezultat în urma complementării un 1 şi reprezentarea finală a numărului întreg negativ -1 pe un octet este 11111111.

În această reprezentare, numărul 00000000 binar reprezintă numărul 0 iar numărul 10000000, care mai înainte reprezenta numărul 0 negativ, acum reprezintă numărul -128. Într-adevăr, numărul 128 se poate reprezenta în binar prin 10000000. Complementat, acest număr devine 01111111 şi după adunarea cu 1, 10000000. Observaţi că numerele 128 şi -128 au aceeaşi reprezentare. Convenţia este aceea că se păstrează reprezentarea pentru -128 şi se elimină cea pentru 128. Alegerea este datorată faptului că toate numerele pozitive au în primul bit valoarea 0 şi toate cele negative valoarea -1. Prin transformarea lui 10000000 în -128 se păstrează această regulă.

Folosind reprezentarea în complement faţă de doi, numerele întregi reprezentabile pe un octet sunt în intervalul -128 până la 127, adică -2⁷ până la 2⁷ -1. În general, dacă avem o configuraţie de n cifre binare, folosind reprezentarea în complement faţă de doi putem reprezenta numerele întregi din intervalul închis -2^n-1 până la 2^n-1-1. În practică, se folosesc numere întregi cu semn reprezentate pe 1 octet, 2 octeţi, 4 octeţi şi 8 octeţi, respectiv 8, 16, 32 şi 64 de biţi.

Dacă dorim să reprezentăm un număr real în memoria calculatorului, o putem face memorând câteva cifre semnificative ale acestuia plus o informaţie legată de ordinul său de mărime. În acest fel, deşi pierdem precizia numărului, putem reprezenta valori foarte aproape de zero sau foarte departe de această valoare.

Soluţia de reprezentare este aceea de a păstra două numere cu semn care reprezintă cifrele semnificative ale numărului real respectiv un exponent care dă ordinul de mărime. Cifrele reprezentative ale numărului se numesc împreună mantisă. Numărul reprezentat în final este 0.mantisaE^exponent. E are valoarea 256 spre deosebire de exponentul 10 pe care îl folosim în uzual. Dacă valoarea exponentului estefoarte mare şi pozitivă, numărul real reprezentat este foarte departe de 0, înspre plus sau înspre minus. Dacă exponentul este foarte mare în valoare absolutăşi negativ, numărul real reprezentat este foarte aproape de zero.

În plus, pentru a ne asigura de biunivocitatea corespondenţei, avem nevoie de o convenţie care să stabilească faptul că virgula este plasată imediat în faţa cifrelor semnificative şi că în faţa acesteia se găseşte o singură cifră 0. Numerele care respectă această convenţie se numesc numere normalizate.

Această mutare a virgulei imediat în faţa cifrelor semnificative poate să presupună modificarea exponentului care păstrează ordinul de mărime al numărului. Numerele fracţionare se numesc în limbajul calculatoarelor numere în virgulă mobilă sau numere flotante tocmai din cauza acestei eventuale ajustări a poziţiei virgulei.

Cu această convenţie nu se poate reprezenta orice număr real, dar se poate obţine o acoperire destul de bună a unui interval al axei numerelor reale cu valori. Atunci când încercăm să reprezentăm în memoria calculatorului un număr real, căutăm de fapt cel mai apropiat număr real reprezentabil în calculator şi aproximăm numărul iniţial cu acesta din urmă. Ca rezultat, putem efectua calcule complexe cu o precizie rezonabilă.

Descrierea convenţiei exacte de reprezentare a numerelor reale în calculator depăşeşte cadrul acestei prezentări. Unele dintre detalii pot fi diferite de cele prezentate aici, dar principiul este exact acesta. Convenţia de reprezentare a numerelor reale este standardizată de IEEE în specificaţia 754.

Desigur, în unele probleme, lipsa de precizie poate să altereze rezultatul final, mai ales că, uneori, erorile se cumulează. Există de altfel o teorie complexă, analiza numerică, concepută pentru a studia căile prin care putem ţine sub control aceste erori de precizie. Putem creşte precizia de reprezentare a numerelor reale prin mărirea spaţiului rezervat mantisei. În acest fel mărim numărul de cifre semnificative pe care îl păstrăm. În general, unităţile centrale actuale lucrează cu două precizii: numerele flotante simple, reprezentate pe 4 octeţi şi numerele flotante duble, reprezentate pe 8 octeţi.

2.3 Valori de adevăr

Uneori, avem nevoie să memorăm în calculator valori de adevăr. Există doar două valori de adevăr posibile: adevărat şi fals. Uneori, aceste valori de adevăr se mai numesc şi valori booleene. Deşi pentru memorarea acestor valori este suficientă o singură cifră binară, în practică aceste valori sunt reprezentate pe un întreg octet pentru că operaţiile la nivel de bit sunt de obicei prea lente. Valorile booleene se pot combina între ele prin operaţii logice: “şi”, “sau”, "negaţie”.

2.4 Şiruri de caractere

După cum spuneam mai înainte, deşi orice informaţie reprezentată în calculator este în final un număr, mintea umană este obişnuită să lucreze cu cuvinte şi imagini mai mult decât cu numere. De aceea, calculatorul trebuie să aibă posibilitatea să simuleze memorarea informaţiilor de acest fel.

În ceea ce priveşte cuvintele, ele pot fi reprezentate în memoria calculatorului prin caracterele care le formează. Înşiruirea acestor caractere în memorie duce la noţiunea de şir de caractere. Pe lângă caracterele propriu-zise care construiesc cuvântul, un şir de caractere trebuie să poată memora şi numărul total de caractere din şir, cu alte cuvinte lungimea sa.

În realitate, un şir de caractere nu conţine doar un singur cuvânt ci este o înşiruire oarecare de caractere printre care pot exista şi caractere spaţiu. De exemplu, următoarele secvenţe sunt şiruri de caractere: "Acesta este un şir de caractere", "Eugen", "ABCD 0123", "HGkduI;.!".

Fiecare limbaj de programare trebuie să ofere o convenţie de reprezentare a şirurilor de caractere în calculator precum şi o convenţie de scriere a acestora în program. De obicei, cea de-a doua convenţie este aceea că şirul de caractere trebuie închis între apostroafe sau ghilimele. În paragraful anterior de exemplu, am folosit ghilimele pentru delimitarea şirurilor de caractere.

Convenţia de reprezentare în memorie diferă de la un limbaj de programare la altul prin modul în care este memorată lungimea şirului, precum şi prin convenţia de reprezentare în memorie a caracterelor: ASCII, Unicode sau alta.

Împreună cu fiecare tip de dată, limbajele de programare trebuie să definească şi operaţiile ce se pot executa cu datele de tipul respectiv. Pentru şirurile de caractere, principala operaţie este concatenarea. Prin concatenarea a două şiruri de caractere se obţine un şir de caractere care conţine caracterele celor două şiruri puse în prelungire. De exemplu, prin concatenarea şirurilor de caractere "unu" şi ", doi", rezultă şirul de caractere: "unu, doi".

2.5 Tipuri primitive de valori ale unui limbaj de programare

Vom numi tipuri primitive de valori ale unui limbaj acele tipuri de valori care se pot reprezenta direct într-un anumit limbaj de programare. Pentru ca informaţia reprezentabilă să fie independentă de calculatorul pe care rulează programele, un limbaj de programare trebuie să-şi definească propriile sale tipuri primitive, eventual diferite de cele ale unităţii centrale, tipuri care să generalizeze tipurile primitive ale tuturor unităţilor centrale.

Pentru fiecare dintre aceste tipuri primitive de valori, limbajul trebuie să definească dimensiunea locaţiei de memorie ocupate, convenţia de reprezentare şi mulţimea valorilor care pot fi reprezentate în această locaţie. În plus, limbajul trebuie să definească operaţiile care se pot executa cu aceste tipuri şi comportarea acestor operaţii pe seturi de valori diferite.

Tipurile primitive ale unui limbaj sunt de obicei: numere de diverse tipuri, caractere, şiruri de caractere, valori de adevăr şi valori de tip referinţă. Totuşi, acest set de tipuri primitive, denumirea exactă a tipurilor şi operaţiile care se pot executa cu ele variază mult de la un limbaj de programare la altul.

2.6 Tablouri de elemente

Tipurile primitive împreună cu referinţele, adică tipurile de date elementare, indivizibile ale unui limbaj, sunt insuficiente pentru necesităţile unei aplicaţii reale. De obicei este nevoie de organizări de date mai complicate în care avem structuri de date create prin asocierea mai multor tipuri de date elementare. Aceste structuri de organizare a informaţiilor pot conţine date de acelaşi tip sau date de tipuri diferite.

În cazul în care dorim să reprezentăm o structură conţinând date de acelaşi tip, va trebui să folosim o structură clasică de reprezentare a datelor numită tablou de elemente. Practic, un tablou de elemente este o alăturare de locaţii de memorie de acelaşi fel. Alăturarea este continuă în sensul că zona de memorie alocată tabloului nu are găuri. De exemplu, putem gândi întreaga memorie internă a calculatorului ca fiind un tablou de cifre binare sau ca un tablou de octeţi.

Informaţiile de acelaşi fel reprezentate într-un tablou se pot prelucra în mod unitar. Referirea la un element din tablou se face prin precizarea locaţiei de început a tabloului în memorie şi a numărului de ordine al elementului pe care dorim să-l referim. Numărul de ordine al unui element se numeşte indexul elementului. De aceea, tablourile se numesc uneori şi structuri de date indexate.

Să presupunem că, la adresa 1234 în memorie, deci începând cu octetul numărul 1234, avem un tablou de 200 de elemente de tip întregi cu semn reprezentaţi pe 4 octeţi. Pentru a accesa elementul numărul 123 din tablou, trebuie să îi aflăm adresa în memorie. Pentru aceasta, trebuie să calculăm deplasamentul acestui element faţă de începutul tabloului, cu alte cuvinte, la câţi octeţi distanţă faţă de începutul tabloului se găseşte elementul numărul 123.

Pentru calcului deplasamentului, este nevoie să ştim cu ce index începe numerotarea elementelor din tablou. De obicei aceasta începe cu 0 sau cu 1, primul element fiind elementul 0 sau elementul 1. Să presupunem, în cazul nostru, că numerotarea ar începe cu 0. În acest caz, elementul cu indexul 123 este de fapt al 124-lea element din tablou, deci mai are încă 123 de elemente înaintea lui. În aceste condiţii, pentru a afla adresa elementului dat, este suficient să adăugăm la adresa de început a tabloului, deplasamentul calculat ca numărul de elemente din faţă înmulţit cu dimensiunea unui element din tablou. Adresa finală este 1234 + 123 * 4 = 1726.

Pentru a putea lucra cu elementele unui tablou este deci suficient să memorăm adresa de început a tabloului şi indexul elementelor pe care dorim să le accesăm. Alternativa ar fi fost să memorăm adresa locaţiei fiecărui element din tablou.

Unul dintre marile avantaje ale utilizării tablourilor este acela că elementele dintr-un tablou se pot prelucra în mod repetitiv, apelându-se aceeaşi operaţie pentru un subset al elementelor din tablou. Astfel, într-un program putem formula instrucţiuni de forma: pentru elementele tabloului T începând de la al treilea până la al N-lea, să se execute operaţia O. Numărul N poate fi calculat dinamic în timpul execuţiei programului, în funcţie de necesităţi.

Elementele unui tablou pot fi de tip primitiv, referinţă sau pot fi tipuri compuse, inclusiv alte tablouri.

2.7 Expresii de calcul

Sarcina principală a calculatoarelor este aceea de a efectua calcule. Pentru a putea efectua aceste calcule, calculatorul trebuie să primească o descriere a operaţiilor de calcul pe care le are de executat. Calculele simple sunt descrise cel mai bine prin expresii de calcul.

Expresiile sunt formate dintr-o serie de valori care intră în calcul, numite operanzi şi din simboluri care specifică operaţiile care trebuiesc efectuate cu aceste valori, numite operatori. Operatorii reprezintă operaţii de adunare, înmulţire, împărţire, concatenare a şirurilor de caractere, etc.

Operanzii unor expresii pot fi valori elementare precum numerele, şirurile de caractere sau pot fi referiri către locaţii de memorie în care sunt memorate aceste valori. Tot operanzi pot fi şi valorile unor funcţii predefinite precum sinus, cosinus sau valoarea absolută a unui număr. Calculul complex al valorii acestor funcţii pentru argumentele de intrare este astfel ascuns sub un nume uşor de recunoscut.

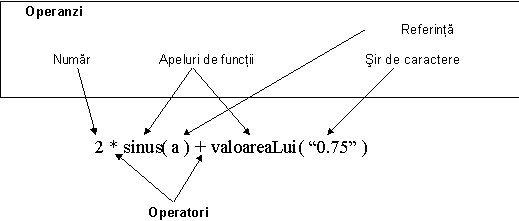
Figura 2.1 Un exemplu de expresie şi componentele acesteia

2.8 Variabile

Uneori, atunci când calculele sunt complexe, avem nevoie să păstrăm rezultate parţiale ale acestor calcule în locaţii temporare de memorie. Alteori, chiar datele iniţiale ale problemei trebuie memorate pentru o folosire ulterioară. Aceste locaţii de memorie folosite ca depozit de valori le vom numi variabile. Variabilele pot juca rol de operanzi în expresii.

Pentru a regăsi valoarea memorată într-o anumită variabilă, este suficient să memorăm poziţia locaţiei variabilei în memorie şi tipul de dată memorată la această locaţie, numit şi tipul variabilei. Cunoaşterea tipului variabilei este esenţială la memorarea şi regăsirea datelor. La locaţia variabilei găsim întotdeauna o configuraţie de cifre binare. Interpretarea acestor cifre binare se poate face numai cunoscând convenţia de reprezentare care s-a folosit la memorarea acelor cifre binare. Mai mult, tipul de variabilă ne şi spune câţi octeţi de memorie ocupă locaţia respectivă.

Pentru a putea referi variabilele în interiorul unui program, trebuie să atribuim câte un nume pentru fiecare dintre acestea şi să rezervăm locaţiile de memorie destinate lor. Această rezervare a locaţiilor se poate face fie la pornirea programului fie pe parcurs.

Putem împărţi variabilele în funcţie de perioada lor de existenţă în variabile statice, care există pe tot parcursul programului şi variabile locale care se creează doar în secţiunea de program în care este nevoie de ele pentru a fi distruse imediat ce se părăseşte secţiunea respectivă. Variabilele statice păstrează de obicei informaţii esenţiale pentru execuţia programului precum numele celui care a pornit programul, data de pornire, ora de pornire sau numărul p . Variabilele locale păstrează valori care au sens doar în contextul unei anumite secţiuni din program. De exemplu, variabilele care sunt utilizate la calculul sinusului dintr-un număr, sunt inutile şi trebuiesc eliberate imediat ce calculul a fost terminat. În continuare, doar valoarea finală a sinusului este importantă.

În plus, există variabile care se creează doar la cererea explicită a programului şi nu sunt eliberate decât atunci când programul nu mai are nevoie de ele. Aceste variabile se numesc variabile dinamice. De exemplu, se creează o variabilă dinamică atunci când utilizatorul programului introduce un nou nume într-o listă de persoane. Crearea şi ştergerea acestui nume nu are legătură cu faza în care se află rularea programului ci are legătură cu dorinţa celui care utilizează programul de a mai adăuga sau şterge un nume în lista persoanelor cu care lucrează, pentru a le trimite, de exemplu, felicitări de anul nou.

2.9 Instrucţiuni

Operaţiile care trebuiesc executate de un anumit program sunt exprimate în limbajele de programare cu ajutorul unor instrucţiuni. Spre deosebire de limbajele naturale, există doar câteva tipuri standard de instrucţiuni care pot fi combinate între ele pentru a obţine funcţionalitatea programelor. Sintaxa de scriere a acestor tipuri de instrucţiuni este foarte rigidă. Motivul acestei rigidităţi este faptul că un compilator recunoaşte un anumit tip de instrucţiune după sintaxa ei şi nu după sensul pe care îl are ca în cazul limbajelor naturale.

Tipurile elementare de instrucţiuni nu s-au schimbat de-a lungul timpului pentru că ele sunt conţinute în însuşi modelul de funcţionare al calculatoarelor Von Neumann.

În primul rând, avem instrucţiuni de atribuire. Aceste instrucţiuni presupun existenţa unei locaţii de memorie căreia dorim să-i atribuim o anumită valoare. Atribuirea poate să pară o operaţie foarte simplă dar realitatea este cu totul alta. În primul rând, valoarea respectivă poate fi rezultatul evaluării (calculului) unei expresii complicate care trebuie executată înainte de a fi memorată în locaţia de memorie dorită.

Apoi, însăşi poziţia locaţiei în memorie ar putea fi rezultatul unui calcul în urma căruia să rezulte o anumită adresă. De exemplu, am putea dori să atribuim o valoare unui element din interiorul unui tablou. Într-o astfel de situaţie, locaţia de memorie este calculată prin adunarea unui deplasament la adresa de început a tabloului.

În fine, locaţia de memorie şi valoarea pe care dorim să i-o atribuim ar putea avea tipuri diferite. În acest caz, operaţia de atribuire presupune şi transformarea, dacă este posibilă, a valorii într-o nouă valoare de acelaşi tip cu locaţia de memorie. În plus, această transformare trebuie efectuată în aşa fel încât să nu se piardă semnificaţia valorii originale. De exemplu, dacă valoarea originală era -1 întreg iar locaţia de memorie este de tip flotant, valoarea obţinută după transformare trebuie să fie -1.0.

Transformarea valorilor de la un tip la altul se numeşte în termeni informatici conversie. Conversiile pot apărea şi în alte situaţii decât instrucţiunile de atribuire, de exemplu la transmiterea parametrilor unei funcţii, în calculul unei expresii.

Forma generală a unei instrucţiuni de atribuire este:

Locaţie = Valoare

Locaţia poate fi o adresă cu tip, un nume de variabilă sau o expresie în urma căreia să rezulte o adresă cu tip. Printr-o adresă cu tip înţelegem o adresă de memorie pentru care a fost specificat tipul valorilor care pot fi memorate în interior. O adresă simplă, fără tip, nu poate intra într-o atribuire pentru că nu putem şti care este convenţia de reprezentare care trebuie folosită la memorarea valorii.

Al doilea tip de instrucţiune elementară este instrucţiunea condiţională. Această instrucţiune permite o primă formă de ramificare a ordinii în care se execută instrucţiunile. Ramificarea depinde de o condiţie care poate fi testată pe setul de date cu care lucrează aplicaţia. În funcţie de valoarea de adevăr care rezultă în urma evaluării condiţiei se poate executa o instrucţiune sau alta. Modelul de exprimare a unei expresii condiţionale este următorul:

Dacă condiţia este adevărată

execută instrucţiunea 1

altfel

execută instrucţiunea 2.

Cele două ramuri de execuţie sunt disjuncte în sensul că dacă este executată instrucţiunea de pe o ramură atunci cu siguranţă instrucţiunea de pe cealaltă ramură nu va fi executată. După execuţia uneia sau a celeilalte instrucţiuni ramurile se reunifică şi execuţia îşi continuă drumul cu instrucţiunea care urmează după instrucţiunea condiţională.

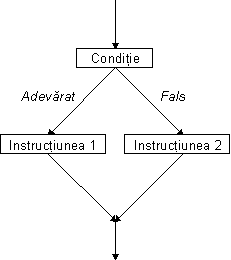
Figura 2.2 Schema de funcţionare a unei instrucţiuni condiţionale

Condiţia care hotărăşte care din cele două instrucţiuni va fi executată este de obicei un test de egalitate între două valori sau un test de ordonare în care o valoare este testată dacă este mai mică sau nu decât o altă valoare. Condiţiile pot fi compuse prin conectori logici de tipul “şi”, “sau” sau “non”, rezultând în final condiţii de forma: dacă variabila numită Temperatură este mai mică decât 0 şi mai mare decât -10, atunci…

Instrucţiunile condiţionale au şi o variantă în care, în funcţie de o valoare întreagă alege o instrucţiune dintr-un set de instrucţiuni şi apoi o execută. Această formă este în realitate derivată din instrucţiunea condiţională clasică, ea putând fi exprimată prin:

Dacă Variabila este egală cu Valoarea 1 atunci

execută instrucţiunea 1

altfel, dacă Variabila este egală cu Valoarea 2 atunci

execută instrucţiunea 2

altfel, dacă Variabila …

…

altfel

execută instrucţiunea implicită.

Un al treilea tip de instrucţiuni elementare sunt instrucţiunile de ciclare sau repetitive sau buclele. Acestea specifică faptul că o instrucţiune trebuie executată în mod repetat. Controlul ciclurilor de instrucţiuni se poate face pe diverse criterii. De exemplu se poate executa o instrucţiune de un număr fix de ori sau se poate executa instrucţiunea până când o condiţie devine adevărată sau falsă.

Condiţia de terminare a buclei poate fi testată la începutul buclei sau la sfârşitul acesteia. Dacă condiţia este testată de fiecare dată înainte de execuţia instrucţiunii, funcţionarea ciclului se poate descrie prin:

Atâta timp cât Condiţia este adevărată

execută Instrucţiunea

Acest tip de instrucţiuni de ciclare poată numele de cicluri while, cuvântul while însemnând în limba engleză "atâta timp cât”. În cazul ciclurilor while, există posibilitatea ca instrucţiunea din interiorul ciclului să nu se execute niciodată, dacă condiţia este de la început falsă.

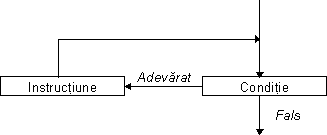
Figura 2.3 Schema de funcţionare a unui ciclu while

Dacă condiţia este testată de fiecare dată după execuţia instrucţiunii, funcţionarea ciclului se poate descrie prin:

Execută Instrucţiunea

atâta timp cât Condiţia este adevărată.

Acest tip de instrucţiuni de ciclare poartă numele de cicluri do-while, cuvântul do însemnând în limba engleză "execută”. În cazul ciclurilor do-while instrucţiunea din interiorul ciclului este garantat că se execută cel puţin o dată, chiar dacă valoare condiţiei de terminare a buclei este de la început fals.

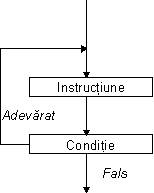
Figura 2.4 Schema de funcţionare a unui ciclu do-while

După cum aţi observat, probabil, dacă instrucţiunea din interiorul buclei nu afectează în nici un fel valoarea de adevăr a condiţiei de terminare a buclei, există şansa ca bucla să nu se termine niciodată.

Al patrulea tip de instrucţiuni sunt apelurile de proceduri. O procedură este o secvenţă de instrucţiuni de sine stătătoare şi parametrizată. Un apel de procedură este o instrucţiune prin care forţăm programul să execute pe loc instrucţiunile unei anumite proceduri. După execuţia procedurii, se continuă cu execuţia instrucţiunii de după apelul de procedură.

Procedurile sunt utile atunci când, în zone diferite ale programului, dorim să executăm aceeaşi secvenţă de instrucţiuni. În aceste situaţii, putem să scriem secvenţa de instrucţiuni o singură dată şi s-o apelăm apoi oriunde din interiorul programului.

De exemplu, ori de câte ori vom dori să ştergem toate semnele de pe ecranul calculatorului, putem apela la o procedură, pentru a nu fi nevoiţi să scriem de fiecare dată secvenţa de instrucţiuni care duce la ştergerea ecranului. Procedura în sine, o vom scrie o singură dată şi îi vom da un nume prin care o vom putea apela ulterior ori de câte ori avem nevoie.

Uneori secvenţa de instrucţiuni dintr-o procedură depinde de nişte parametri adică de un set de valori care sunt precizate doar în momentul apelului procedurii. În aceste cazuri, procedura se poate comporta în mod diferit în funcţie de valorile de apel ale acestor parametri. În funcţie de tipul declarat al unor parametri şi de tipul real al valorilor care sunt trimise ca parametri într-un apel de procedură, se poate întâmpla ca înainte de apelul propriu-zis să fie necesară o conversie de tip.

De exemplu, în cazul procedurii care calculează valoarea sinusului unui număr, parametrul de intrare este însuşi numărul pentru care trebuie calculat sinusul. Rezultatul acestui calcul va fi diferit, în funcţie de valoarea la apel a parametrului. În mod normal, parametrul va fi un număr flotant iar dacă la apel vom transmite ca parametru o valoare întreagă, ea va fi convertită spre o valoare flotantă.

În urma apelului unei proceduri poate rezulta o valoare pe care o vom numi valoare de retur a procedurii. De exemplu, în urma apelului procedurii de calcul a sinusului unui număr, rezultă o valoare flotantă care este valoarea calculată a sinusului. Acest tip de proceduri, care întorc valori de retur se mai numesc şi funcţii. Funcţiile definesc întotdeauna un tip al valorii de retur pe care o întorc. În acest fel, apelurile de funcţii pot fi implicate şi în formarea unor expresii de calcul sub formă de operanzi, expresia cunoscând tipul de valoare care trebuie aşteptată ca valoare a apelului unei anumite funcţii.

Analogia cu funcţiile pe care le-aţi studiat la matematică este evidentă dar nu totală. În cazul funcţiilor scrise într-un limbaj de programare, două apeluri consecutive ale aceleiaşi funcţii cu aceleaşi valori ca parametri se pot comporta diferit datorită dependenţei de condiţii exterioare sistemului format din funcţie şi parametrii de apel. În plus, se poate întâmpla ca modul de comportare al funcţiei şi valoarea de retur să nu fie definite pentru anumite valori de apel ale parametrilor. Deşi scrierea acestui tip de funcţii este nerecomandabilă, în practică întâlnim astfel de funcţii la tot pasul.