CÂTEVA RELAŢII METRICE ÎN PATRULATERUL OARECARE ŞI ÎN TETRAEDRU

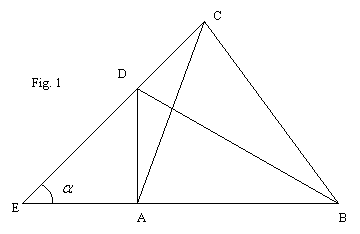
Fie ABCD un patrulater oarecare. Ne propunem sa evaluăm pentru început unghiul format de două laturi opuse, folosind funcţia trigonometrică cos.

Cu notaţiile din figura 1 vom demonstra următoarea relaţie

(1)

Vom scrie pentru început următoarea relaţie vectorială:

. Ridicăm la pătrat această relaţie vectorială şi obţinem:

Am ţinut cont de egalităţile:

Explicitând din această relaţie se obţine relaţia:

Observaţie: Această relaţie poate fi considerată ca un fel de teorema cosinusului pentru patrulatere.

Ca aplicaţie pentru această relaţie propunem următoarea:

1) Să se arate că într-un patrulater oarecare ABCD are loc inegalitatea:

Soluţie: Se observă mai întâi că având se obţine:

, cu egalitate dacă adică AB//CD.

Analog se poate scrie că: , cu egaliate din nou când CB//AD. Adunând cele două relaţii se obţine relatia din enunţ.

Egalitatea are loc dacă ABCD este paralelogram.

Ne propunem în continuare să evaluăm unghiul format de diagonalele patrulaterului ABCD.

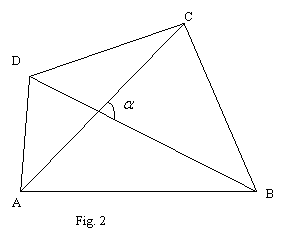
Cu notaţiile din figura 2 putem scrie:

Ridicăm această relaţie vectorială la pătrat obţinem:

Am ţinut cont de egalităţile:

Din relaţia precedentă prin explicitarea lui se obţine următoarea relaţie:

(2)

Observaţie: Obţinem ca o consecinţă următorul rezultat cunoscut:

Un patrulater ABCD are diagonalele AC şi BD perpendiculare dacă şi numai dacă:

Urmând un procedeu similar în cazul unui tetraedru oarecare ABCD, cu notaţiile din figura 3 vom avea: , (3) unde prin se înţelege unghiul dreptelor AB şi CD.

Vom scrie relaţia vectorială: , care după ridicare la pătrat devine:

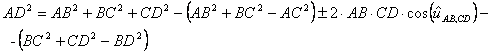
Întrucât ne referim la unghiul ascuţit al dreptelor AB şi CD se va alege semnul corespunzător în faţa produsului . Prin separarea acestui produs şi trecerea la modul se obţine:

.

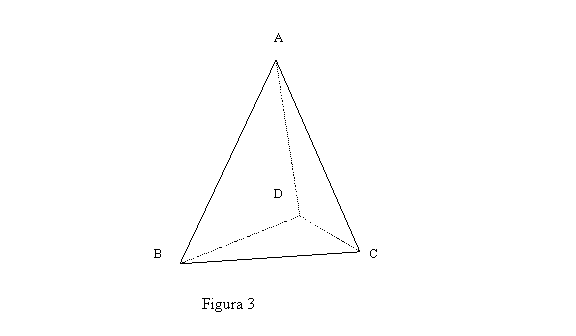
Observaţie: Analog putem obţine: şi

De aici se obţine o foarte cunoscută problemă care zice că:

Muchiile opuse ale unui tetraedru ABCD sunt perpendiculare dacă şi numai dacă:

Dacă considerăm acum ABCD un tetraedru echifacial, se ştie că acesta are muchiile opuse congruente. Dacă notăm AB=CD=a, AC=BD=b, BC=AD=c, se va obţine:

, şi

Se poate arăta acum că dacă laturile opuse într-un tetraedru echifacial formează unghiuri congruente atunci tetraedru este regulat. În particular, dacă laturile opuse în tetraedru echifacial sunt perpendiculare atunci tetraedru este regulat.

Într-adevăr, dacă de exemplu am avea atunci rezultă că:

. Dacă atunci ceea ce este fals. Prin urmare vom avea neapărat şi ţinând cont de ipoteză rezultă a=b=c ceea ce demonstrează afirmaţia.