Relaţii metrice fundamentale

Vom considera mai întâi figura de mai jos:

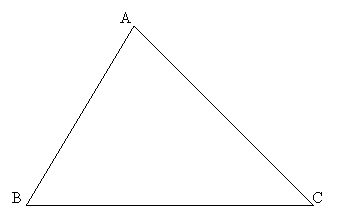
Fig 1.

La baza tuturor relaţiilor metrice fundamentale stă de fapt o relaţie vectorială.

Fundamental la acest capitol mi se pare relaţia:

(1)

Dacă la figura de mai sus mai punem şi o oblică aşa cum se vede în figura 2 se demonstrează foarte uşor relaţia vectorială:

(2)

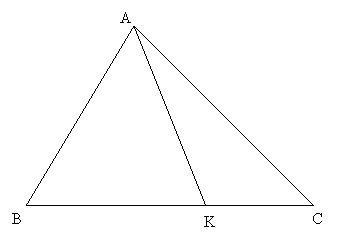
Fig 2

Rapoartele reprezintă coordonatele vectorului în baza formată de vectorii . Dacă notăm aceste rapoarte cu atunci relaţia (2) se mai scrie: (3).

Ridicând relaţia (3) la pătrat şi ţinând cont de relaţia 1 se va obţine:

După câteva calcule simple relaţia:

(4) care nu este altceva decât relaţia lui Stewart.

Mergând după acest model şi considerând figura 3 se ştie următoarea relaţie vectorială:

(5)

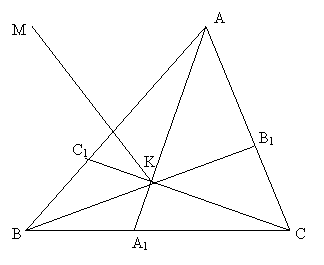
Fig. 3

Interesant este că relaţia (5) este de fapt o relaţie valabilă în spaţiu, iar rapoartele: reprezintă coordonatele vectorului în baza determinată de vectorii

Ridicând relaţia (5) la pătrat se obţine relaţia:

, (6) relaţie de o importanţă deosebită în geometrie.

Din această relaţie decurg exprimări pentru distanţele de la un punct oarecare al planului la puncte importante în triunghi. De exemplu:

1) unde G este centrul de greutate al triunghiului.

2) , unde a, b, c sunt lungimile laturilor triunghiului ABC iar I este centrul cercului înscris triunghiului ABC.

Consecintele relaţiei (6) sunt numeroase dar nu trebuie uitată nici posibilitatea de a aplica relaţia 6 în spaţiu în cazul tetraedrului.