Două teoreme de concurenta la patrulatere.

Vom face la început pentru uşurinţa expunerii câteva convenţii. Deasemenea vom reaminti câteva teoreme utile în redactarea materialului de faţă. Fie K un punct aparţinând segmentului [AB]. Vom nota: iar atunci cand între A şi B nu mai avem fixate şi alte puncte vom nota pur şi simplu: .

Observaţie: Este evident că . Cu aceste notaţii putem să reamintim:

Teorema lui Ceva: Fie ABC un triunghi şi. Dreptele AA₁, BB₁, CC₁ sunt trei drepte concurente dacă şi numai dacă: . (1)

Observaţie: Se observă că relaţia (1) este echivalentă cu relaţia:

ceea ce poate constitui o “regula” de înmulţire a acestui tip de rapoarte.

În teorema lui Ceva am considerat doar cazul când toate punctele sunt in interiorul laturilor însă rezultatele care urmează nu vor fi influenţate de această condiţie. Vom mai reaminti şi teorema lui Van Aubel:

Teorema Van Aubel : Fie ABC un triunghi şi AA₁, BB₁, CC₁ trei drepte concurente în punctul K, conform cu figura 1.

Fig. 1.

În aceste condiţii: .

Vom trece acum la enunţarea primei teoreme de concurenţă:

Teorema 1: Fie ABCD un patrulater. Dacă M, N, P, Q, R, S sunt puncte respectiv pe segmentele: [AB], [BC], [CD], [DA], [AC], [BD] astfel încât cevienele corespunzătoare din triunghiurile ABC, BCD şi CDA sunt concurente atunci şi cevienele din triunghiul DAB sunt concurente (fig 2).

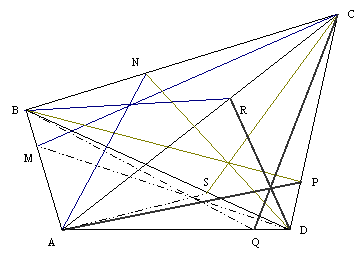
Fig. 2

Demonstraţie: Cu notaţiile anterioare vom scrie că:

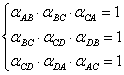şi va trebui să demonstrăm că: Din relaţiile anterioare rezultă exprimările: care conduc imediat la rezultat.

Teorema 2: Fie ABCD un patrulater. Dacă M, N, P, Q, R, S sunt puncte respectiv pe segmentele: [AB], [BC], [CD], [DA], [AC], [BD] astfel încât cevienele corespunzătoare din triunghiurile ABC, BCD şi CDA şi DAB sunt concurente respectiv în punctele: atunci dreptele sunt concurente. (fig. 3)

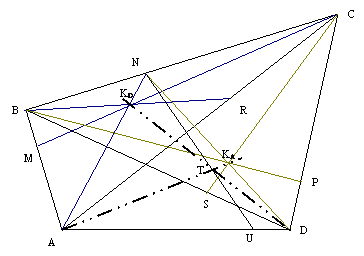
Fig. 3

Demonstraţie: Am considerat o figură simplificată intenţia fiind aceia de a arăta că segmentul [AK_A] este tăiat de segmentele de la vârfurile vecine (DK_D şi BK_B) în acelaşi raport fapt care ne conduce la concluzia ca oricare trei din cele 4 segmente sunt concurente şi de aici concluzia că toate cele 4 drepte sunt concurente.

Cu notaţiile anterioare şi cele din figura 3 vom avea conform cu teorema lui Van Aubel:

şi . Referindu-ne strict la triunghiul AND vom putea scrie: 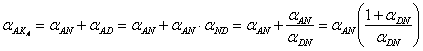sau:

sau: (2).

Relaţia precedentă ne spune că segmentul DK_D taie segmentul AK_A într-un raport egal cu suma rapoartelor care pleaca din vârful A proprietate care o va avea evident şi segmentul BK_B şi deci segmentele AK_A, BK_B şi DK_D sunt concurente şi conform cu observaţiile de la început rezultă concluzia.

Observaţie: Relaţia: ar putea fi privita ca o relaţie de tip Van Aubel pentru patrulatere.

Teorema precedentă este valabilă şi în spaţiu adică se poate spune că:

Propoziţie: Dacă M, N, P, Q, R, S sunt 6 puncte respectiv pe laturile: [AB], [BC], [CD], [DA], [AC], [BD] ale unui tetraedru ABCD astfel încât cevienele corespunzătoare din fetele ABC, BCD şi CDA şi DAB sunt concurente respectiv în punctele: atunci dreptele sunt concurente.

Demonstraţia în spaţiu este foarte simplă pentru că în spaţiu oricare două din cele 4 drepte sunt concurente şi oricare 3 sunt necoplanare de unde rezultă ca toate 4 vor fi concurente. Rămâne însă de interes relaţia Van Aubel pentru tetraedru care are o exprimare asemănătoare cu relaţia (2).

Stăniloiu Nicolae, prf. Bocşa