Calculul unor sume cu combinări

Sunt bine cunoscute egalităţi ca:

1)

2)

3)

Vom da o metodă de calcul pentru sume mai generale de forma: , unde gr(P)=p.

Mai întâi voi enunţa un rezultat cunoscut fără să-l mai demonstrez.

Fie polinoamele .

Propoziţia 1: Dacă P este un polinom de grad , atunci există constantele reale astfel încât:

.

Observaţie: Propoziţia precedentă exprimă faptul că polinoamele reprezintă o bază pentru spaţiul vectorial al polinoamelor de grad cel mult p.

Propoziţia 2: , pentru orice .

Demonstraţie: Se observă că: şi atunci:

.

Observaţie: În sumele anterioare combinările care apar cu indice superior negativ le considerăm nule.

Propoziţia 3: Dacă P este un polinom de grad p atunci există un polinom F de grad cel mult p astfel încât:

Demonstraţie: Conform cu propoziţia 1 există astfel încât:

şi atunci:

Este clar acum că şi că

Propoziţia 3 ne dă dreptul să elaborăm următoarea metodă de calcul al sumelor de tipul: unde .

Se încearcă determinarea polinomului F de grad p a.î luând pentru n suficiente valori.

În numărul 24 al RMCS apare la clasa X-a problema 113 care cere calculul sumei: . Evident şi gr(P)=3. Presupunem .

În egalitatea: , dăm lui n valorile 3, 4, 5 şi 6 şi obţinem: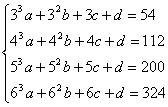

Determinantul sistemului de mai sus este de tip Vandermonde iar rezolvarea acestuia nu ar trebui sa fie o problemă. Se obţine a=1, b=3, c=0, d=0. şi deci:

Ca metodă alternativă pentru calculul sumei putem aminti următoarea metodă la nivelul clasei XI-a:

Se pleacă de la dezvoltarea:

. Se derivează o data în raport cu x iar egalitatea obţinută se înmulţeste cu x, apoi se repetă procedeul de două ori şi apoi se ia x=1.

Stăniloiu Nicolae, prf. Bocşa