Inegalităţi

- material pentru clasa a VII-a –

· Metoda directă – constă în efectuarea calculelor şi transformarea inegalităţilor aduse la forma cea mai simplă după care se foloseşte ipoteza sau proprietatea (A-B)²≥0 sau faptul că o sumă de pătrate este mai mare sau egală cu 0.

1. Dacă aR, atunci a²+1≥2a.

2. Dacă aR^*₊ , atunci .

3. Dacă a, b, cR, atunci a²+b²+c²≥ab+bc+ca.

(Ind. Inmulţim inegalitatea cu 2 şi grupăm astfel încât să obţinem o sumă de pătrate ≥0).

· Metoda reducerii la absurd

4. Dacă a, b, c(0,1) să se demonstreze că cel puţin unul din numerele a(1-b), b(1-c), c(1-a) este mai mic sau egal cu .

(Indicaţie: Presupunem că a(1-b), b(1-c), c(1-a) sunt mai mari decât . Facem produsul lor şi regrupăm după a(1-a)> , facem calcule şi obţinem (A-B)²<0 deci inegalitate falsă).

· Metodă bazată pe implicaţii

şi , unde a, b, c, d sunt numere reale. Inegalitatea devine egalitate dacă şi numai dacă a=b şi c=d

şi , unde a, b, c, d sunt numere reale pozitive. Inegalitatea devine egalitate dacă şi numai dacă a=b şi c=d.

Aceste inegalităţi sunt valabile şi în cazul a n inegalităţi.

5. a) Să se demonstreze că : ,

b) Să se determine pentru care este verificată egalitatea:

(Indicaţie: a), adunând n obţineţi membrul stâng, formaţi si membrul drept şi obţineţi inegalitatea; b) se aplică a) pt. n=1, 2, ...).

6. Fie numerele şi .

a) determinaţi o relaţie între a şi b;

b) arătaţi că a<1;

c) arătaţi că b<.

(Indicaţie: b) calculaţi , c) analog)

7. Să se arate că: , pentru orice număr natural n≥1.

(Indicaţie: notati x= şi inegalitatea se transformă într-o inegalitate simplu de demonstrat)

· Metoda bazată pe reducerea la o inegalitate cunoscută sau înlocuirea în inegalităţi cunoscute

Inegalităţi remarcabile:

1. Inegalitatea lui Bernoulli

Fie a≥-1, n, atunci

2. Inegalitatea mediilor:0< min(a,b)≤m_h≤m_g≤m_a≤m_p≤max(a,b)

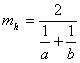(media armonică); (media geometrică); (media aritmetică);

(media pătratică)

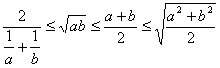
Şi dacă 0<a<b, atunci a<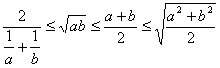< b (egalitatea are loc dacă a=b).

3. Identitatea lui Lagrange

sau

4. Inegalitatea lui Cauchy-Buniakovski-Schwarz (CBS)

sau

În general:

5. Inegalitatea lui Minkovski

6. Inegalitatea lui Cebâşeav

I. Dacă a₁≤ a₂≤...≤ a_n şi b₁≤ b₂≤...≤ b_n,

Atunci:

II. Dacă a₁≤ a₂≤...≤ a_n şi b₁≥ b₂≥...≥ b_n,

Atunci:

8. Dacă a,b,cR, atunci:

(Indicaţie: aplicaţi inegalitatea lui Minkovski)

9. Dacă a,b,cR₊, atunci

(Indicaţie: aplicaţi inegalitatea mediilor)

10. Fie 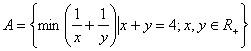şi

şi a este minim}. Calculaţi aria patrulaterului determinat de elementele mulţimii xB.

(Indicaţie: aplicaţi inegalitatea mediilor pt.m_h şi m_a)

11. Dacă a, b, c, u, v sunt numere pozitive şi u+v≥2, arătaţi că:

a)

b)

c)

Indicaţie:

a) Se arată că şi cum u+v≥2 rezultă concluzia.

b) Aplicând CBS se obţine inegalitatea cerută

c) Folosind a) şi b) se obţine: , de unde concluzia este imediată.

12. Fie a,b cu proprietatea . Să se arate că

(Indicaţie: aplicaţi inegalitatea mediilor m_h şi m_g pentru b² şi , c² şi , a² şi ).

13. Să se demonstreze că pentru orice numere reale pozitive au loc inegalităţile:

a) , b) , c) , d) , e) ,

f) , g) , h)

i) (ind.: aplicaţi g)); j) ; l)dacă a+b+c=1, atunci

14. Se dă expresia ,

a) Să se simplifice expresia E; b) Să se demonstreze că

15. Fie a, b, c numere reale astfel încât a+b+c=6p. Să se demonstreze că a²+b²+c²≥12p².

16. Fie a, b, c lungimile laturilor unui .

a) Să se determine natura dacă are loc relaţia

b) Dacă c are valoare constantă, iar expresia (p-a)(p-b) are valoare maximă, să se demonstreze că triunghiul este isoscel (s-a notat cu p semiperimetrul triunghiului).

17. a) Să se demonstreze că dintre toate dreptunghiurile cu acelaşi perimetru, pătratul are aria maximă,

b) Să se demonstreze că dintre toate dreptunghiurile cu aceeaşi arie, pătratul are perimetrul minim,

c) Fie a lungimea ipotenuzei unui triunghi dreptunghic, iar S aria sa. Să se demonstreze că dacă , atunci triunghiul este isoscel.

Indicaţie:

a) Fie a,b dimensiunile dreptunghiului şi P-perimetrul, A-aria

Din (inegalitatea mediilor), condiţia de maxim este echivalent cu condiţia de egalitate)

b) P=2a+2b≥=4; perimetrul este minim dacă a=b, deci dreptunghiul este pătrat;

c) Ridicând relaţia dată la pătrat şi aplicând teorema lui Pitagora, obţineţi cerinţa.